pading

from Crypto.Util.number import \*
import gmpy2
flag = b'SHCTF{\*\*\*\*\*\*\*\*}'
assert len(flag) == 39
p = getPrime(512)
q = getPrime(512)
n = p \* q
e = 0x3
pad = b'a\_easy\_problem'
c = pow(bytes\_to\_long(flag + pad), e, n)
print(f'n = {n}')
print(f'c = {c}')
'''
n = 55802474004832948449028131952560698215358744234394538813097711801512368271243550182034446343259853556823765206933248497103051171383392204222119217729067443452072452467969242945362014030389150081066873547217944887590171478793204015983131600770850692066482373764437716870132063439456149741167249034859974608933
c = 10676267451763449910318794892231703485018191930863480542635292280013700411207364299058281444186070873277655117787688698365750004677877369565103400534344529888229149029478185463185679756207142716279940072863233482543169971719661520570902887576301476082077309423381359222218785057784497102270754372247920218617
'''

flag为39bytes，pad为14bytes，共53bytes，大概53x8=424位, e=3，则$m^e$大概有424x3=1272位，n为1024位 由$m^e-c=k\*n$可得到k为248位=>无法直接开e次方和k值爆破

使用coppersmith攻击：(条件:$X^e<n$)

构造方程：$f=(x+pad)^e-c \\mod n$，求其small_root

代码实现(sage)：

from Crypto.Util.number import \*
from sage.all import \*
n = 55802474004832948449028131952560698215358744234394538813097711801512368271243550182034446343259853556823765206933248497103051171383392204222119217729067443452072452467969242945362014030389150081066873547217944887590171478793204015983131600770850692066482373764437716870132063439456149741167249034859974608933
c = 10676267451763449910318794892231703485018191930863480542635292280013700411207364299058281444186070873277655117787688698365750004677877369565103400534344529888229149029478185463185679756207142716279940072863233482543169971719661520570902887576301476082077309423381359222218785057784497102270754372247920218617
e = 3
pad = bytes\_to\_long(b'a\_easy\_problem')
P.<x> = PolynomialRing(Zmod(n))
f =((x\*2\*\*(14\*8)+pad)^3 - c).monic() 
#x\*2\*\*(14\*8)+pad是为了满足上方的bytes\_to\_long(flag + pad)
print(long\_to\_bytes(int(f.small\_roots(X=2\*\*(39\*8),beta=0.5,epsilon=0.01)\[0])))

得到结果：b'SHCTF{ArE_YoU_paDDDlNg_mE_b0Y_1gbEAGIG}'

EzAES

from Crypto.Cipher import AES
import os

iv = os.urandom(16)
key = os.urandom(16)
my\_aes = AES.new(key, AES.MODE\_CBC, iv)
flag = open('flag.txt', 'rb').read()
flag += (16 - len(flag) % 16) \* b' '
c = my\_aes.encrypt(flag)
print(c)
print(iv)
print(key)
'''
b'\\x9c\\xa3\\xb62g\\xbfmr\\xf8\\x8d\\xedV\\xea\\x99\\x8bW\\xc5\\xd0\\x97\\xb4J\_6\\x15,>\\xae\\xef\\xb2\\x13U-c\\xa4<\\x865\\xe8m\\x8b\\x94\\xe1\\x9d\\xa9\\x97\\xdc\\x15?'
b'\\x03\\xd5H\\xcf?\\xe4\\xb3\\x0b^3\\xff\\x00blJ\\x8a'
b'\\x8f\\xdeQ\\xd9\\x9b;\\xdaz\\xc3\\xeb\\x17ka\\xcbT\\xdf'
'''

直接写代码：

from Crypto.Cipher import AES

iv=b'\\x03\\xd5H\\xcf?\\xe4\\xb3\\x0b^3\\xff\\x00blJ\\x8a'
key=b'\\x8f\\xdeQ\\xd9\\x9b;\\xdaz\\xc3\\xeb\\x17ka\\xcbT\\xdf'
c=b'\\x9c\\xa3\\xb62g\\xbfmr\\xf8\\x8d\\xedV\\xea\\x99\\x8bW\\xc5\\xd0\\x97\\xb4J\_6\\x15,>\\xae\\xef\\xb2\\x13U-c\\xa4<\\x865\\xe8m\\x8b\\x94\\xe1\\x9d\\xa9\\x97\\xdc\\x15?'

my\_aes\_decrypt = AES.new(key, AES.MODE\_CBC, iv)
print(my\_aes\_decrypt.decrypt(c))
得到：b'SHCTF{66c4f53b-80f7-4c93-a42e-451e0344b8ee}\\x00\\x00\\x00\\x00\\x00'
Hello Crypto | SOLVED | nanxer
from Crypto.Util.number import bytes\_to\_long
from secret import flag

m = bytes\_to\_long(flag)
print("m =",m)

# In cryptography, m stands for message, also plaintext
# so, why this m is number?
# decrypt this Message to get flag!
# m = 215055650564999509150865773761787614220832480906972200398989904374196869215378126546418066872115465113865391469332646933629

转一下就ok

from Crypto.Util.number import long\_to\_bytes
m=215055650564999509150865773761787614220832480906972200398989904374196869215378126546418066872115465113865391469332646933629
print(long\_to\_bytes(m))

得到：b'SHCTF{heLlO_c7f3r_wE1c0me_t0_crypTo_WoRID_34G3D7e4}'

factor

from Crypto.Util.number import \*
import random
from enc import flag

m = bytes\_to\_long(flag)
e = 65537
def prod(iterable):
    result = 1
    for num in iterable:
        result \*= num
    return result
prime\_list = \[getPrime(64) for \_ in  range(10) ]
N = prod(prime\_list)
p\_list = random.sample(prime\_list,7)
n = prod(p\_list)
c = pow(m,e,n)
print(f"c = {c}")
print(f"N = {N}")
'''
c = 27716701068485773067829482765418396739208215525424227518924106597748142715817928081915741684665830416329345733437644659780060969709811
N = 576622794578672066177194581265358997867617097282232171904938283410137008869469369549184811893313840410490871847261049634458319113934556518433109933070705771504470900643200090743802676379947257
'''

由代码知，N为10个64位的素数相乘，分解N:

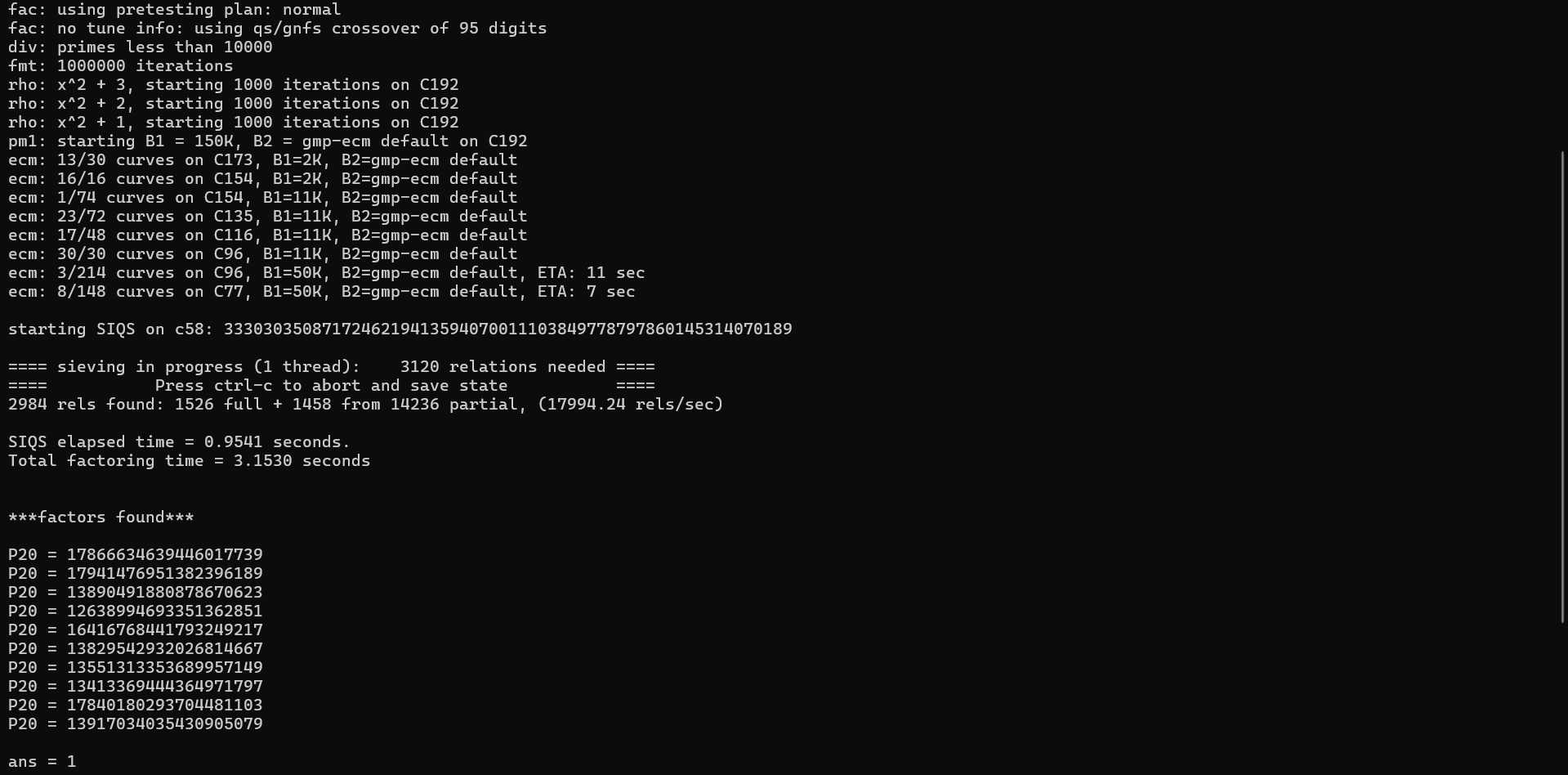
得到：

P20 = 17866634639446017739
P20 = 17941476951382396189
P20 = 13551313353689957149
P20 = 16416768441793249217
P20 = 13917034035430905079
P20 = 13890491880878670623
P20 = 17840180293704481103
P20 = 12638994693351362851
P20 = 13829542932026814667
P20 = 13413369444364971797

n位N中任意7个的组合，使用itertools->>combinations遍历

from Crypto.Util.number import \*
from itertools import combinations

e = 65537
def prod(iterable):
    result = 1
    for num in iterable:
        result \*= num
    return result

c0 = 27716701068485773067829482765418396739208215525424227518924106597748142715817928081915741684665830416329345733437644659780060969709811
prime\_list =\[17866634639446017739,17941476951382396189,13551313353689957149,16416768441793249217,13917034035430905079,13890491880878670623,17840180293704481103,12638994693351362851,13829542932026814667,13413369444364971797]

phi\_N = 1
for p in prime\_list:
    phi\_N \*= p-1
d = inverse(e, phi\_N)
c= combinations(prime\_list, 7)
for p\_list in c:
    if b'SHCTF{' in long\_to\_bytes(pow(c0,d,prod(p\_list))):
        print(long\_to\_bytes(pow(c0,d,prod(p\_list))))

得到flag:b'SHCTF{79187267-31cb-4a40-8db2-715e5b06f750}'

上一页TGCTF2025

下一页鹏城杯2024