0xGame2024

约 582 字大约 2 分钟

2024-12-29

code

题目：

#How to use mathematics to represent information?
from Crypto.Util.number import bytes_to_long
from base64 import b64encode
from secret import flag
msg = flag.encode()
length = len(msg)
assert length%4 == 0
block = length//4
m = [ msg[ block*(i) : block*(i+1) ] for i in range(4) ]
m0 = m[0]
m1 = bytes_to_long(m[1])
m2 = m[2].hex()
m3 = b64encode(m[3])
print(f'm0 = {m0}\nm1 = {m1}\nm2 = {m2}\nm3 = {m3}')
'''
m0 = b'0xGame{73d7'
m1 = 60928972245886112747629873
m2 = 3165662d393339332d3034
m3 = b'N2YwZTdjNGRlMX0='
'''

写代码：

from Crypto.Util.number import long_to_bytes
from base64 import b64encode,b64decode
m0 = b'0xGame{73d7'
m1 = 60928972245886112747629873
m2 = '3165662d393339332d3034'
m3 = b'N2YwZTdjNGRlMX0='
m11=long_to_bytes(m1)
m22=bytes.fromhex(m2)
m33=b64decode(m3)
print(m0+m11+m22+m33)

得到flag 0xGame{73d72f64-7656-11ef-9393-047f0e7c4de1}

Caesar Cipher

检测caesar情况：

a='0yHbnf{Uif_Cfhjoojoh_Pg_Dszqup}'
b='0xGame'
for i in range(len(b)):
    print(ord(a[i])-ord(b[i]))
#输出：
#0
#1
#1
#1
#1
#1

常规加密：

a='0yHbnf{Uif_Cfhjoojoh_Pg_Dszqup}'
b=''
for i in range(len(a)):
    if ('a'<=a[i] and a[i]<='z') or ('A'<=a[i] and a[i]<='Z'):
        b+=chr(ord(a[i])-1)
    else:
        b +=a[i]
print(b)
#输出：
#0xGame{The_Beginning_Of_Crypto}

RSA-Baby

题目：

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd
#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()
#RSA AlgorithmParameter Generation Function:
def KeyGen():
    Factor_BitLength = 30
    q = getPrime(Factor_BitLength)
    p = getPrime(Factor_BitLength)
    N = p * q
    #Euler's totient function:
    phi = (p-1) * (q-1)
    #Generate Keys:
    while True:
        e = randint(1,phi)
        if gcd(e,phi) == 1:
            d = int(invert(e,phi))
            break
    #Generate Result:
    Pub_Key = (N,e)
    Prv_Key = (N,d)
    return Pub_Key,Prv_Key
Pub,Prv = KeyGen()
N = Pub[0]
e = Pub[1]
d = Prv[1]
#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)
print(f'Pub_Key = {Pub}')
print(f'Prv_Key = {Prv}')
print(f'Encrypt_msg = {c}')
'''
Pub_Key = (547938466798424179, 80644065229241095)
Prv_Key = (547938466798424179, 488474228706714247)
Encrypt_msg = 344136655393256706
'''
flag = '0xGame{'+ MD5(m) +'}'

修改：

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd
def MD5(m):return md5(str(m).encode()).hexdigest()
Pub = (547938466798424179, 80644065229241095)
Prv = (547938466798424179, 488474228706714247)
c=344136655393256706
N = Pub[0]
d = Prv[1]
m=pow(c,d,N)
flag = '0xGame{'+ MD5(m) +'}'
print(flag)
#输出
#0xGame{6e5719c54cdde25ce7124e280803f938}

RSA-Easy

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd
#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()
#RSA AlgorithmParameter Generation Function:
def KeyGen():
    Factor_BitLength = 30
    q = getPrime(Factor_BitLength)
    p = getPrime(Factor_BitLength)
    N = p * q
    #Euler's totient function:
    phi = (p-1) * (q-1)
    #Generate Keys:
    while True:
        e = randint(1,phi)
        if gcd(e,phi) == 1:
            break
    #Generate Result:
    Pub_Key = (N,e)
    return Pub_Key
Pub = KeyGen()
N = Pub[0]
e = Pub[1]
#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)
print(f'Pub_Key = {Pub}')
print(f'Encrypt_msg = {c}')
'''
Pub_Key = (689802261604270193, 620245111658678815)
Encrypt_msg = 289281498571087475
'''
flag = '0xGame{'+ MD5(m) +'}'

分解N：

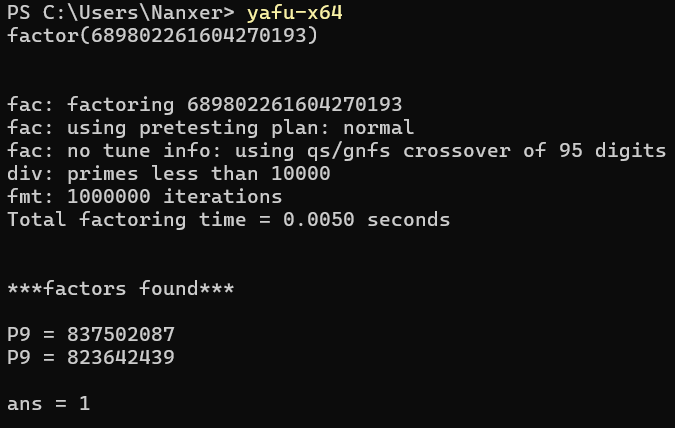
计算d：

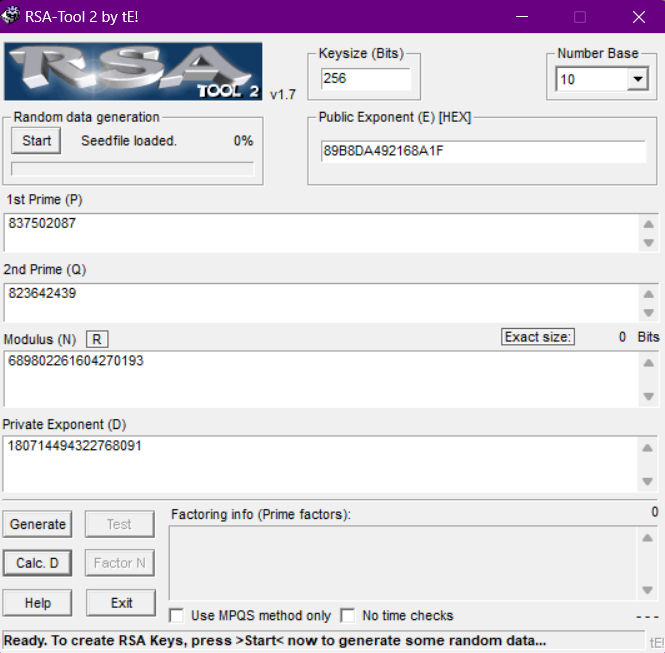
计算：

from hashlib import md5
def MD5(m):return md5(str(m).encode()).hexdigest()
Pub = (689802261604270193, 620245111658678815)
N = Pub[0]
c=289281498571087475
d=180714494322768091
m=pow(c,d,N)
flag = '0xGame{'+ MD5(m) +'}'
print(flag)
#输出
#0xGame{5aa4603855d01ffdc5dcf92e0e604f31}